Service virtualization is growing in popularity. There are many solutions to different types of problems in that space. Unfortunately, there is still a lot of confusion on how service virtualization compares to stubbing and mocking. Testers’ and developers’ points of views are still different. This article is an attempt to help bring order and structure to your day to day activities. After reading the article, you will have solid foundations to lead conversations with your peers.
If you have heard about mocking, stubbing and service virtualization before, but would like to deepen your knowledge this article is for you. If you have not heard about service virtualization yet, have a look at the quick introduction to service virtualization.Taking a step back, what is a test double?
It all starts with Test Doubles. A test double allows us to decouple yourself from your dependencies when testing the system under test (SUT). You replace the dependency with an equivalent interface that allows you to exercise a given test case.
The most common categories of a test double used by developers are (examples in brackets):
- dummy object (a string “John” or a constant integer 12345)
- stub (a StubHttpResponse class that always returns the same response “OK”)
- spy (a SpyHttpResponse class that records all invocations of the onGet method)
- fake (a FakeDatabase class which persists to an in memory H2 database instead of an expensive production-like instance of Oracle)
- mock (a dynamic proxy implementation of UserListener interface, implemented by Mockito and used in a unit test)
The most common categories of a test double used by QAs are (examples in brackets):
- stub (a servlet in a WAR file created using SoapUI and deployed to a remote Tomcat instance at http://testEnviroment1.mycompany.com:8080/getWeatherService)
- virtual service (an artifact created with a service virtualization tool and deployed to a remote shared virtual service enviromenent at http://vs-enviroment.mycompany.com:18034/getWeatherService)
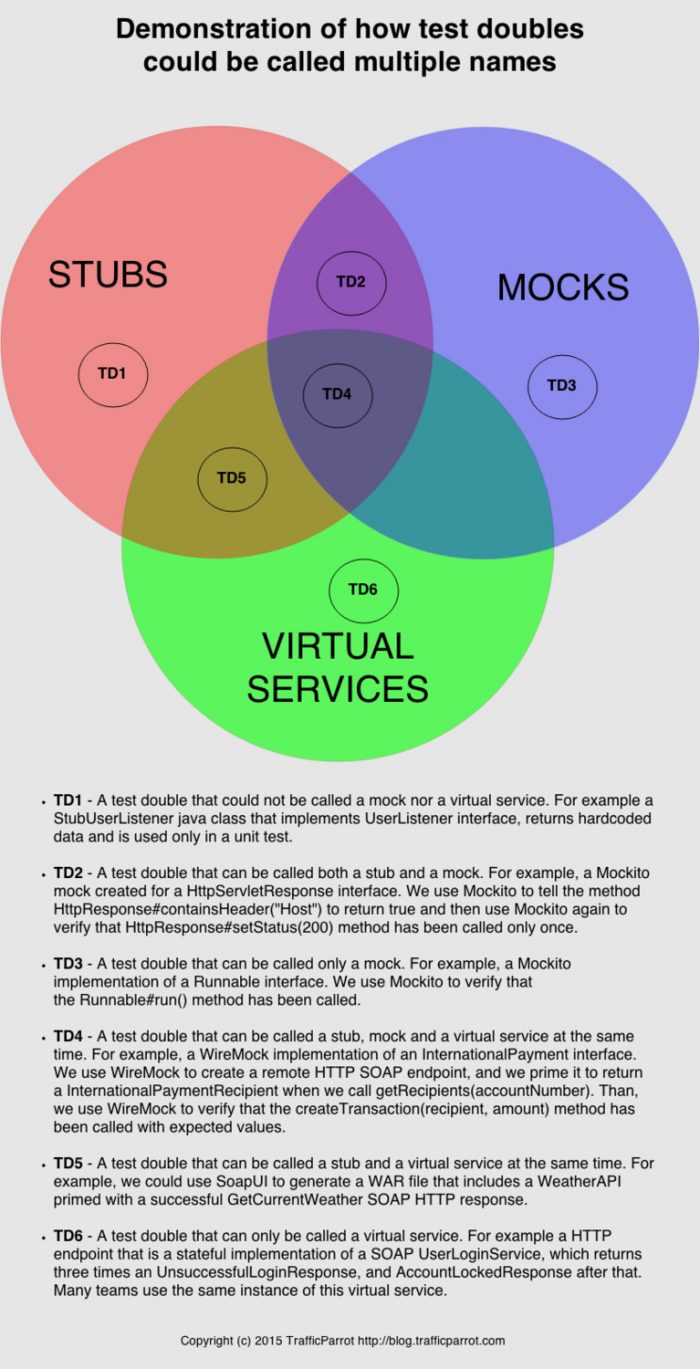
It is often also hard to say which of the following categories a test double fits into. They should be treated as spectrums rather than strict definitions. For example, a given test double could be considered as a stub and a spy at the same time.
Mock vs. Stub vs. Virtual Service
The most commonly discussed categories of test doubles are mocks, stubs and virtual services.
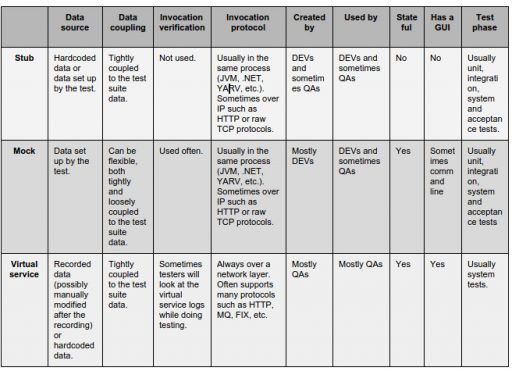
A stub is a minimal implementation of an interface, usually returning hardcoded data. The hardcoded data is tightly coupled to the test suite. The tests are going to depend on that data. It is most useful when the suite of tests is simple, and keeping the hardcoded data in the stub is not an issue. Some stubs are handwritten, some can be generated by tools for you. Some developers will say that a stub can also be primed, but you cannot verify an invocation on a stub.
A mock usually verifies outputs against expectations. Those expectations are set in the test. It is also most often created by using a third party library, for example in Java that is Mockito, JMock or WireMock. It is most useful when you have a large suite of tests and the stub is not enough, because each of the tests needs different data set up. Maintaining a stub in that case could be costly, so you can use a mock instead. Also, the verification the mock does is a useful tool from a developers point of view when writing automated tests. On top of that, a mock focuses on interactions rather than state. Mocks are usually stateful, for example you can verify how many times a given method was called.
That is the main difference between a mock and a stub, from a developer’s point of view.
A virtual service is a test double usually provided as SaaS, often created by recording traffic rather than building from scratch based on documentation. It is created using one of the service virtualization platforms. Those tools establish a common ground for teams to communicate and facilitate artifact sharing. Stubs and mocks on the other hand are usually written by developers, occasionally shared with QAs and very rarely shared with other development teams due to the interoperability problems (different software platforms, deployment infrastructures, etc.). Often the service virtualization tools support many protocols (HTTP, MQ, TCP, etc.), whereas stubs and mocks frequently support only one. Most of the service virtualization tools have GUIs. It is another approach to stubbing on a larger scale, bringing QAs to the table as well. Virtual services are always called remotely (over HTTP, TCP, etc.) whereas stubs and mocks most often work in-process directly with classes, methods and functions. This means virtual services are typically used for system testing but stubs and mocks for unit/module/acceptance testing. A virtual service can be considered a stub on steroids. Often, you will see an instance of a virtual service deployed in an environment used by many teams simultaneously, whereas stubs would be individual instances per team.
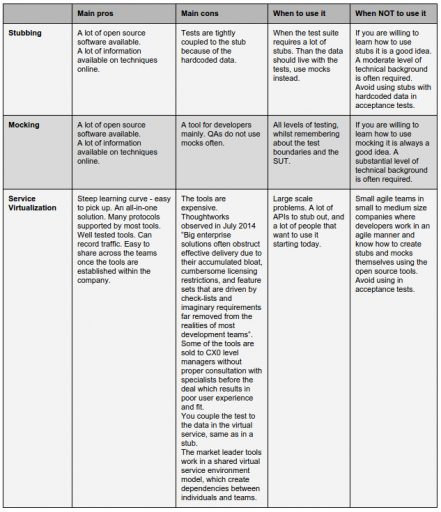
All of the approaches mentioned above come with pros and cons. We will have a look at those later.
Download report comparing 40+ service virtualization tools.
What is Service Virtualization?
It is the practice of creating virtual services and sharing them across teams. Developers and testers working on the same product can use the same virtual service artifacts or even virtual services. Another example is QA teams across a large enterprise using the same virtual service artifacts. It promotes communication between DEV and QA teams across many departments. It also attempts to address the problem of duplicated efforts by creating stubs for the same APIs within a large organisation by many teams simultaneously. It is a glorified stub, that can be stateful. All of that comes with a cost as usual, we will look at that later.
Is service virtualization better than stubbing and mocking?
Is using an electric screwdriver better than using a small manual one? It depends on the job you need to to. The small manual screw driver works very well when you need to disassemble your laptop, which is very fragile and requires careful handling. The electric screw driver works very well if you have got a wooden furniture set and you need to assemble it yourself. It is a bit more expensive than the manual one as well. That means it is best to have both of those tools in your toolbox.
Similar with service virtualization, stubs and mocks. They solve different problems. Some problems can be addressed by both stubs, mocks and virtual services. Some problems should be addressed only with mocks and stubs. To highlight only a few of the most common concerns please have a look at the comparison below.
Which problems can be addressed by service virtualization but not by stubbing nor mocking?
If you are in a team or organisation where nobody has ever done much stubbing or mocking and you would like to see return on investment quickly writing stubs yourself especially if you are a QA can be a daunting task. That is why there are tools that have GUIs so that you get can get up to speed quickly. Also, they are extensible, which provides flexibility once you get comfortable with the subject. Some of the the service virtualization tools can help you achieve that. So, if you need something to get up to speed quickly, but need the flexibility once you are there, the service virtualization tools might be helpful.
Also, if you are running an organisation with a top-down waterfall approach to software development, with the IT department treated as a cost centre rather than the core of the business (which is inadvisable, because it is has proved many times to be a failed software development approach and even enterprise scale organisations are moving away from it), you can use the service virtualization tools as another governed and recommended tool for your organisation. You can use some of those tools as a tactical quick win, whilst you get your organisation in a place where it can be mature enough to consider other approaches.
You need to be careful though. According to the ThoughtWorks Technology Radar big enterprise solutions are getting worse at supplying what users need. Often, it is best to go with the targeted simple solutions rather than bloated enterprise platforms, one like Traffic Parrot if you need to deploy it on your own infrastructure, or for example Sandbox when you are looking for a SaaS solution.
A few random examples
Here are a few examples to give you a better idea of when we could use a stub, mock or a virtual service. The list is just to give you an idea of the possible scenarios. It is not extensive in any way.
I would use a stub when for example:
- I am a backend developer working on a small new application that uses a third party library to communicate with an external API. I would then create an interface in my code that will decouple me from that third party library. One implementation of that interface would use the third party library classes and would be used in an end to end test. The other implementation would be a stub that would return hardcoded values, and would be used in my unit tests.
- I am a tester and I need to test the application my team is working on in isolation. I would create a stub for the HTTP RESTfull APIs the application depends on using in house built tools provided to me by our team’s developers.
I would use a mock when for example:
- I am a backend developer working on a fairly large application and I need to decouple myself from my HTTP API dependencies. I would use a remote mocking framework such as WireMock or moutebank and prime the mocks in the acceptance tests.
- I am a backend developer and I am working with a codebase with thousands of class unit tests. I would use Mockito to mock the dependency classes in my tests.
I would use a virtual service when for example:
- I am a developer working on a very large complex legacy application that has many dependencies, with test coverage that is less than 3%. Also, the dependencies of the system are unavailable 60% of the time. I would use a service virtualization tool to create virtual services by recording the traffic. That would help me decoule myself from the downtime of the dependencies. I would also let my testers use those virtual services. This would be a short term tactical solution before I spend the time on creating an automated suite of tests for my application, that would not use recorded but primed data.
- I am a frontend developer working with a public SOAP Weather API. I would use Sandbox to generate the virtual service for me using a WSDL file. I would set up the test data in the virtual service so that all my test cases are being represented, like for example temperatures below -60°C which are never being returned from the real Weather API.
- I am a NFT tester responsible for performance of a large banking application. I would use tcpdump to record incoming and outgoing traffic in production for a day. Than I would import the outgoing traffic using a service virtualization tool and create a virtual service. I would import the incoming traffic to JMeter using tcpreplay and JMeter Proxy. I would run a test suite in my performance environment using JMeter, and use the virtual services to decouple myself from dependencies. I would repeat the recording process every week.
How do I start doing service virtualization, stubbing or mocking today?
A good overview of stubs and mocks can be found in the the GooS book. If you are a software developer try using Mockito to learn how to do do mocking. If you are a software tester try doing stubbing using TrafficParrot or SoapUI MockService. It’s also worth reviewing any of the enterprise vendors like CA, IBM or Parasoft but as ThoughtWorks observed in Jan 2014 most of the innovation comes from practitioners contributing to open source.
Need more help?
Contact me:
- contact@wbsoftwareconsultancy.com
- +44 793 88 47 800
- http://trafficparrot.com
Original article: http://blog.trafficparrot.com/2015/05/what-is-difference-between-stub-mock.html
Is this article for you? Service virtualization is growing in popularity. There are many solutions to different types of problems in that space.
来源: What is the difference between a stub, a mock and a virtual service?